و ترتبط عادة الحركة بجملة مقارنة مرتبطة بالمسار . 


 حيث أن السرعة العددية  :
$$v=\frac{{}_{}^{}d{s}_{}^{}}{dt}=(s){\text{'}}_t$$
$$\overrightarrow{a_{}}=\overrightarrow{a_T}+\overrightarrow{a_C}$$

•  المركبة المماسية :

•  المركبة الناظمية : 

$$a_C=\frac{{}_{}^{}{v}^2}{r}$$

$$a=\sqrt{a_T{}^2+a_C{}^2}$$

تعرف الفاصلة الزاوية بأنها القياس الجبري للزاوية المركزية المقابل للفاصلة أي الزاوية المحصورة بالمبدأو المركز و الموضع جبرياً ..: 

$$\theta =\widehat{OCN}$$ وترتبط الفاصلة الزاوية بالفاصلة الخطية بالعلاقة : 
$$\theta =\frac{{}_{}{s}_{}}{r}\begin{array}{ccc}& \iff & \end{array}s=r.\theta$$ $$$$$$$$ ب- السرعة الزاوية : 

• تعرف السرعة الزاوية الوسطى بأنها معدل تغير الفاصلة الزاوية بمرور الزمن : 

$${\omega }_{avg}=\frac{\Delta \theta }{\Delta t}=\frac{{\theta }_2-{\theta }_1}{t_2-t_1}$$

• أما السرعة الزاوية اللحظية فهي المعدل الموافق لانتقال صغير خلال زمن صغير و تساوي مشتق الفاصلة الزاوية بالنسبة للزمن : 

$$\omega =\frac{d\theta }{dt}=\left(\theta \right){\text{'}}_t$$

• ويعبر عن السرعة الزاوية شعاعياً   بشعاع السرعة الزاوية "شعاع الدوران" بشعاع ينطبق على محور الدوران يتجه باتجاه ابهام يد يمنى تلتف أصابعها بجهة الحركة . 

• وترتبط السرعة الزاوية بالسرعة الخطية : 

$$\omega =\frac{{}_{}{v}_{}}{r}\begin{array}{ccc}& \iff & \end{array}v=r.\omega$$
$$$$

• يعرف التسارع الزاوي  الوسطي بأنه معدل تغير السرعة الزاوية بمرور الزمن : 

$${\alpha }_{avg}=\frac{\Delta \omega }{\Delta t}=\frac{{\omega }_2-{\omega }_1}{t_2-t_1}$$

• أما التسارع الزاوي اللحظي  فهو المعدل الموافق لتغير صغير في السرعة الزاوية  خلال زمن صغير و تساوي مشتق السرعة الزاوية و المشتق الثاني للفاصلة الزاوية بالنسبة للزمن : 

$$\alpha =\frac{d\omega }{dt}=\left(\omega \right){\text{'}}_t=\left(\theta \right)\text{'}{\text{'}}_t$$

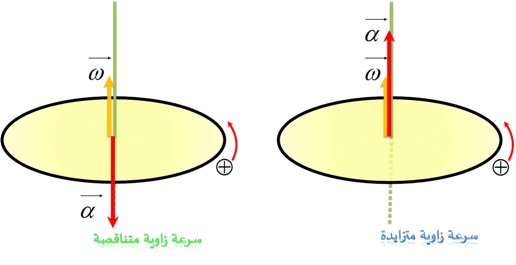
• ويعبر شعاعياً عن التسارع الزاوي بشعاع التسارع الزاوي الذي ينطبق على محور الدوران متجه باتجاه شعاع السرعة الزاوية المتزايدة وبعكس اتجاه شعاع السرعة الزاوية المتناقصة . 

• ويرتبط التسارع الزاوي بالتسارع المماسي  :

$$\alpha =\frac{{}_{}{a}_T}{r}\begin{array}{ccc}& \iff & \end{array}{a}_T=r.\alpha$$